Ratio, Proportion & Alligation
Example 1: If p:q = r:s = t:u = 2:3, then (mp + nr + ot) : (mq + ns + ou) is equal to?
Solution: We know that, If a/b = c/d = e/f, then these ratios will be equal to = (a+c+e/b+d+f)
Here, p/q = r/s = t/u = 2/3
⇒ mp/mq = nr/ns = ot/ou = 2/3
⇒ (mp + nr + ot)/(mq + ns + ou) = 2/3 or 2:3
Here, p/q = r/s = t/u = 2/3
⇒ mp/mq = nr/ns = ot/ou = 2/3
⇒ (mp + nr + ot)/(mq + ns + ou) = 2/3 or 2:3
Example 2: If A:B = 3:4, B:C = 5:7 and C:D = 8:9 then A:D is equal to?
Solution: To find A:D, either we can find common ratio A:B:C:D (check here how to find it) or we can simply multiply and get answer quickly.
⇒ A/B x C/D x E/F = 3/4 x 5/7 x 8/9
⇒ A/D or A:D = 10/21 or 10:21
⇒ A/B x C/D x E/F = 3/4 x 5/7 x 8/9
⇒ A/D or A:D = 10/21 or 10:21
Example 3: A milkman makes 20% profit by selling milk mixed with water at Rs 9 per litre. If the cost price of 1 litre pure milk is Rs 10, then the ratio of milk and water in the mixture is?
Example 4: The ratio of present age of two brothers is 1:2 and 5 years back the ratio was 1:3. What will be the ratio of their age after 5 years?
Solution: Method 1: Let present age be x and 2x years.
Then 5 years back ratio = (x - 5)/(2x - 5) = 1/3
⇒ 3x - 15 = 2x - 5
⇒ x = 10 years
Age of elder brother = 2x = 20 years.
Ratio after 5 years will be = (10 + 5) : (20 + 5) = 3:5
Method 2: We know that, A ratio is not altered by multiplying or dividing both its terms by the same number.
Ratio Five years back = 1 : 3
Present Ratio = 1:2 or we can write 2 : 4
Both the ratios increased by 1 in 5 years
It means Difference of ratio = 5 years
⇒ Present age of younger brother = 2 x 5 = 10 years
⇒ Present age of elder brothers = 4 x 5 = 20 years
⇒ Ratio after 5 years = (10 + 5)/(20 + 5) = 3:5
Then 5 years back ratio = (x - 5)/(2x - 5) = 1/3
⇒ 3x - 15 = 2x - 5
⇒ x = 10 years
Age of elder brother = 2x = 20 years.
Ratio after 5 years will be = (10 + 5) : (20 + 5) = 3:5
Method 2: We know that, A ratio is not altered by multiplying or dividing both its terms by the same number.
Ratio Five years back = 1 : 3
Present Ratio = 1:2 or we can write 2 : 4
Both the ratios increased by 1 in 5 years
It means Difference of ratio = 5 years
⇒ Present age of younger brother = 2 x 5 = 10 years
⇒ Present age of elder brothers = 4 x 5 = 20 years
⇒ Ratio after 5 years = (10 + 5)/(20 + 5) = 3:5
Example 5: The ratio of age of father and his son 10 year hence will be 5:3, while 10 year ago it was 3:1. The ratio of the age of the son to that of his father at present?
Solution: By method of Ratios:
Ratio of age 10 years ago : F-10 : S-10 = 3 : 1
Ratio of age 10 years hence : F+10 : S+10 = 5 : 3
Both the ratios are increased by 2 in 20 years.
⇒ 1 = 10 years.
⇒ Age of father 10 years ago = 30 ; Age of son 10 years ago = 10
Ratio of present age = (10+ 10) : (30 + 10) = 1:2
Ratio of age 10 years ago : F-10 : S-10 = 3 : 1
Ratio of age 10 years hence : F+10 : S+10 = 5 : 3
Both the ratios are increased by 2 in 20 years.
⇒ 1 = 10 years.
⇒ Age of father 10 years ago = 30 ; Age of son 10 years ago = 10
Ratio of present age = (10+ 10) : (30 + 10) = 1:2
Example 6: When a particular number is subtracted from each of 7, 9, 11 and 15, the resulting numbers are in proportion. The number to be subtracted is: a.) 1 b.) 2 c.) 3 d.) 5?
Solution: Method 1: Direct formula: In case of number is subtracted from A, B, C and D to make all four quantities in proportion, number will be = (AD - BC)/[(A+D) – (B+C)]
Therefore, number = (7 x 15 – 9 x 11)/[(7 + 15) - (9 + 11)] = 6/2 = 3
Method 2: Going through given options mentally:
(7 – x)/(9 – x) = (11 – x)/(15 - x)
Now going through options, clearly putting x = 3 will give each ratio 2:3
Therefore, number = (7 x 15 – 9 x 11)/[(7 + 15) - (9 + 11)] = 6/2 = 3
Method 2: Going through given options mentally:
(7 – x)/(9 – x) = (11 – x)/(15 - x)
Now going through options, clearly putting x = 3 will give each ratio 2:3
Example 7: Which number when added to each of the numbers 6, 7, 15, 17 will make the resulting numbers proportional: a.) 6 b.) 5 c.) 4 d.) 3?
Solution: Method 1: Direct formula: In case of number is added to A, B, C and D to make all four quantities in proportion, number will be = (BC - AD)/[(A+D) – (B+C)
Therefore, number = (7 x 15 – 6 x 17)/[(6 + 17) - (7 + 15)] = 3/1 = 3
Method 2: Going through given options mentally as in above example.
Therefore, number = (7 x 15 – 6 x 17)/[(6 + 17) - (7 + 15)] = 3/1 = 3
Method 2: Going through given options mentally as in above example.
Example 8: Find the number which when added to the terms of the ratio 11:23 makes it equal to the ratio 4:7?
Solution: Method 1: Direct formula: To convert ratio a:b to c:d by adding any number, number will be = (AD - BC)/(C - D)
Therefore, number = (11 x 7 – 23 x 4)/(4 - 7) = 5
Method 2: In this method we have to change the second ratio in such a way that:
Antecedent of (final ratio – initial ratio) = Consequent of (final ratio – Initial ratio) = Required number to be added
Initial ratio = 11:23
Final ratio = (4:7) x 4 = 16:28
⇒ (16 – 11) = 5 & (28 – 23) = 5 is the required number
Therefore, number = (11 x 7 – 23 x 4)/(4 - 7) = 5
Method 2: In this method we have to change the second ratio in such a way that:
Antecedent of (final ratio – initial ratio) = Consequent of (final ratio – Initial ratio) = Required number to be added
Initial ratio = 11:23
Final ratio = (4:7) x 4 = 16:28
⇒ (16 – 11) = 5 & (28 – 23) = 5 is the required number
Example 9: Find the number which when subtracted from the terms of the ratio 11:23 to make it equal to the ratio 3:7?
Solution: Method 1: Direct formula: To convert ratio a:b to c:d by subtracting any number, number will be = (BC - AD)/(C - D)
Therefore, number = (23 x 3 – 11 x 7)/ (3 - 7) = 2
Method 2: In this method we have to change the second ratio in such a way that:
Antecedent of (initial ratio – final ratio) = Consequent of (initial ratio – final ratio) = Required number to be subtracted
Initial ratio = 11:23
Final ratio = (3:7) x 3 = 9:21
⇒ (11 – 9) = 2 & (23 – 21) = 2 is the required number
Therefore, number = (23 x 3 – 11 x 7)/ (3 - 7) = 2
Method 2: In this method we have to change the second ratio in such a way that:
Antecedent of (initial ratio – final ratio) = Consequent of (initial ratio – final ratio) = Required number to be subtracted
Initial ratio = 11:23
Final ratio = (3:7) x 3 = 9:21
⇒ (11 – 9) = 2 & (23 – 21) = 2 is the required number
Example 10: If there is a reduction in the number of workers in a factory in the ratio 15:11 and an increment in their wage in the ratio 22:25, then the ratio by which the total wage of the workers should be decreased is?
Solution: Required ratio = 15 x 22 : 11 x 25 = 6:5
Example 11: The average marks obtained by 40 students of a class is 86. If the highest marks are removed, the average reduces by one mark. The average marks of the top 5 students is?
Solution: Method 1: Basic: Income of A and B = 3x and 2x
Expenditure of A and B = 5y and 3y.
Saving = Income – Expenditure
⇒ 3x – 5y = 2000……… eq 1.
⇒ 2x – 3y = 2000……….eq 2.
After solving equation 1 and 2, we get x = 4000 and y= 2000
Therefore, income of A = 3x = Rs 12000
income of B = 2x = Rs 8000
Method 2: Formula based: If incomes of two persons are in the ratio a:b and their expenditures are in the ratio c:d, and each of them saves Rs X, then:
Income of first person = Xa(d-c)/(ad-bc) ; Expenditure of first person = Xc(b-a)/(ad-bc)
Income of second person = Xb(d-c)/(ad-bc); Expenditure of second person = Xd(b-a)/(ad-bc)
Putting the values in above formula, we get:
Income of A = [2000 x 3(3-5)]/(3 x 3 – 2 x 5) = Rs 12000
Income of B = [2000 x 2(3-5)]/ (3 x 3 – 2 x 5) = Rs 8000
Method 3: Quickest way by comparing ratios: Income = 3:2 and Expenditure = 5:3
Now saving is: Income – Expenditure, we have to change the ratio in such a way that income – expenditure for both A and B will be same.
Income = (3:2) x 2 = 6: 4
Expenditure = 5:3
⇒ (6 - 5) = 1 = (4 - 3)
It means 1 unit change in ratio is equal to Rs 2000.
Therefore A’s income = 6 x 2000 = Rs 12000
B’s income = 4 x 2000 = Rs 8000
Expenditure of A and B = 5y and 3y.
Saving = Income – Expenditure
⇒ 3x – 5y = 2000……… eq 1.
⇒ 2x – 3y = 2000……….eq 2.
After solving equation 1 and 2, we get x = 4000 and y= 2000
Therefore, income of A = 3x = Rs 12000
income of B = 2x = Rs 8000
Method 2: Formula based: If incomes of two persons are in the ratio a:b and their expenditures are in the ratio c:d, and each of them saves Rs X, then:
Income of first person = Xa(d-c)/(ad-bc) ; Expenditure of first person = Xc(b-a)/(ad-bc)
Income of second person = Xb(d-c)/(ad-bc); Expenditure of second person = Xd(b-a)/(ad-bc)
Putting the values in above formula, we get:
Income of A = [2000 x 3(3-5)]/(3 x 3 – 2 x 5) = Rs 12000
Income of B = [2000 x 2(3-5)]/ (3 x 3 – 2 x 5) = Rs 8000
Method 3: Quickest way by comparing ratios: Income = 3:2 and Expenditure = 5:3
Now saving is: Income – Expenditure, we have to change the ratio in such a way that income – expenditure for both A and B will be same.
Income = (3:2) x 2 = 6: 4
Expenditure = 5:3
⇒ (6 - 5) = 1 = (4 - 3)
It means 1 unit change in ratio is equal to Rs 2000.
Therefore A’s income = 6 x 2000 = Rs 12000
B’s income = 4 x 2000 = Rs 8000
Example 12: Rs 180 contained in a box consists of one rupee, 50 paise and 25 paise coins in the ratio 2:3:4. What is the number of 50 paise coins?
Solution: To convert 50 paise & 25 paise coins into rupees we need to multiply ratio by ½ & ¼ respectively.
Ratio of coins = 2:3:4
⇒ Ratio of value of coins in Rupees = 2x1 : 3x1/2 : 4x1/4 = 4:3:2
Total value of coins = Rs 180
⇒ Value of 50 paise coins = (3x180)/9 = Rs 60
Rs 60 means 120 coins of 50 paise
Ratio of coins = 2:3:4
⇒ Ratio of value of coins in Rupees = 2x1 : 3x1/2 : 4x1/4 = 4:3:2
Total value of coins = Rs 180
⇒ Value of 50 paise coins = (3x180)/9 = Rs 60
Rs 60 means 120 coins of 50 paise
Example 13: If 378 coins consist of rupees, 50 paise and 25 paise coins, whose values are in the ratio of 13:11:7, the number of 50 paise coins will be?
Solution: To convert value of 50 paise & 25 paise coins into number of coins multiply ratio by 2 & 4 respectively.
Ratio of value of coins = 13:11:7
⇒ Ratio of number of coins = 13x1 : 11x2 : 7x4 = 13:22:28
Sum of ratios = 63
⇒ Total number of coins = 378
Number of 50 paise coins = 22x378/63 = 132
Ratio of value of coins = 13:11:7
⇒ Ratio of number of coins = 13x1 : 11x2 : 7x4 = 13:22:28
Sum of ratios = 63
⇒ Total number of coins = 378
Number of 50 paise coins = 22x378/63 = 132
Example 14: A man has in all Rs 640 in the denominator of one rupee, five rupee and ten rupee notes. The number of each type of notes are equal. What is the total number of notes he has?
Solution: Let number of each type of notes be x.
Value of notes will be in Ratio = x : 5x : 10x
Total value = Rs 640
⇒ x + 5x + 10x = 640
⇒ x = 40
Total number of notes are = 40 + 40 + 40 = 120
Value of notes will be in Ratio = x : 5x : 10x
Total value = Rs 640
⇒ x + 5x + 10x = 640
⇒ x = 40
Total number of notes are = 40 + 40 + 40 = 120
Example 15: A policeman starts to chase a thief. When the thief goes 10 steps the policeman moves 8 steps. 5 steps of the policeman is equal to 7 steps of the thief. The ratio of the speeds of the policeman and the thief is?
Solution: 5 steps of policeman = 7 steps of the thief
⇒ 1 step of policeman = 7/5 steps of the thief
⇒ 10 steps of policeman = 7x10/5 = 14 steps of the thief
Therefore, ratio of speed of policeman to the speed of thief = 10 steps of policeman: 8 steps of thief = 14:8 = 7:4
⇒ 1 step of policeman = 7/5 steps of the thief
⇒ 10 steps of policeman = 7x10/5 = 14 steps of the thief
Therefore, ratio of speed of policeman to the speed of thief = 10 steps of policeman: 8 steps of thief = 14:8 = 7:4
Example 16: In 30 litres mixture of acid, the ratio of acid and water is 2:3. What amount of water should be added to the mixtures o that the ratio of acid and water becomes 2:5?
Solution: Method 1: Initial ratio = 2:3 and final ratio = 2:5
Here fixed quantity is acid, so we need to equal the value of fixed quantity in both the ratios. As we have '2' as a value of acid in both the ratios so value is already equal.
Water to be added = (Total quantity of mixture) x (Difference in the ratio of varying quantity)/(Sum of initial ratios)
⇒ 30 x 2/5 = 12 litres
Method 2: Direct formula: If in x litres mixture of milk and water, the ratio of milk and water is a:b, the quantity of water to be added in order to make this ratio c:d = x(ad-bc)/c(a+b)
Putting values in this formula we get = 30(2x5 – 3x2)/ 2(2+3) = 12 litres
Method 3: Initial ratio = 2:3 and Mixture = 30 litres
Acid = 2x30/5 = 12 Litres ; Water = 3x30/5 = 18 litres
Final ratio = 2:5
Here fixed quantity is acid because we added water to change ratio, as value of acid in final mixture is "2", it means: 2x = 12 litres or x = 6 litres
It means water = 5x = 5x6 = 30 litres
Initially water was 18 litres and now 30 litres, it means water added = 30 – 18 = 12 Litres
Method 4: By Alligation: Acid : Water = 2: 3
Water in the original mixture = 3x100/5 = 60%
Water to be added is pure = 100%
Water in resulting mixture = 5x100/7 = (500/7)%
Original mixture mixed with water in the ratio = 200:80 = 5:2
In 5 litres of mixture water to be added is 2 litres
Therefore in 30 litres of mixture water to be added = 30 x 2/5 = 12 litres
Here fixed quantity is acid, so we need to equal the value of fixed quantity in both the ratios. As we have '2' as a value of acid in both the ratios so value is already equal.
Water to be added = (Total quantity of mixture) x (Difference in the ratio of varying quantity)/(Sum of initial ratios)
⇒ 30 x 2/5 = 12 litres
Method 2: Direct formula: If in x litres mixture of milk and water, the ratio of milk and water is a:b, the quantity of water to be added in order to make this ratio c:d = x(ad-bc)/c(a+b)
Putting values in this formula we get = 30(2x5 – 3x2)/ 2(2+3) = 12 litres
Method 3: Initial ratio = 2:3 and Mixture = 30 litres
Acid = 2x30/5 = 12 Litres ; Water = 3x30/5 = 18 litres
Final ratio = 2:5
Here fixed quantity is acid because we added water to change ratio, as value of acid in final mixture is "2", it means: 2x = 12 litres or x = 6 litres
It means water = 5x = 5x6 = 30 litres
Initially water was 18 litres and now 30 litres, it means water added = 30 – 18 = 12 Litres
Method 4: By Alligation: Acid : Water = 2: 3
Water in the original mixture = 3x100/5 = 60%
Water to be added is pure = 100%
Water in resulting mixture = 5x100/7 = (500/7)%
Original mixture mixed with water in the ratio = 200:80 = 5:2
In 5 litres of mixture water to be added is 2 litres
Therefore in 30 litres of mixture water to be added = 30 x 2/5 = 12 litres
Example 17: A can contains a mixture of two liquids A and B in the ratio 7:5. When 9 litres of mixture are drawn off and the can is filled with B, the ratio of A and B becomes 7:9. Litres of liquid A contained by the can initially was?
Solution: Method 1: Basic: Let Liquid A = 7x and Liquid B = 5x. When 9 litre of mixtures are drawn off, liquid A remains = 7x – 9 x 7/12 = 7x – 21/4
Liquid B remains = 5x – 9 x 5/12 = 5x – 15/4
After adding 9 litres of Liquid B new ratio is 7:9.
⇒ (7x – 21/4) : (5x – 15/4) = 7:9
After solving we get x = 3
Quantity of liquid A = 7x = 7 x 3 = 21 litres
Method 2: Direct Formula:
Common factor of first ratio = (Quantity replaced)/sum of terms in first ratio + (quantity replaced x antecedent of first ratio)/sum of terms in first ratio
Putting values, common factor x = (9/12) + (9 x 7/28) = 3
⇒ Quantity of A = 7 x 3 = 21 litres
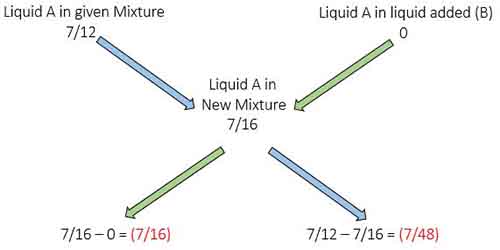
Method 3: By Alligation:
Fraction of A in given mixture = 7/12
Fraction of A in the liquid Added = 0 (since pure liquid B is added)
Fraction of A in the new mixture = 7/16
Ratio of original mixture to B = 7/16 : 7/48 = 3:1
It means for 1 litre of liquid B added, quantity of mixture should be 3 litres.
⇒ For 9 litres of liquid B, original mixture should be = 9 x 3 = 27 litres.
Therefore initial quantity of mixture in can = 27 + 9 = 36 litres.
⇒ A = 7 x 36/12 = 21 litres
⇒ B = 5 x 36/12 = 15 litres
Liquid B remains = 5x – 9 x 5/12 = 5x – 15/4
After adding 9 litres of Liquid B new ratio is 7:9.
⇒ (7x – 21/4) : (5x – 15/4) = 7:9
After solving we get x = 3
Quantity of liquid A = 7x = 7 x 3 = 21 litres
Method 2: Direct Formula:
Common factor of first ratio = (Quantity replaced)/sum of terms in first ratio + (quantity replaced x antecedent of first ratio)/sum of terms in first ratio
Putting values, common factor x = (9/12) + (9 x 7/28) = 3
⇒ Quantity of A = 7 x 3 = 21 litres
Method 3: By Alligation:
Fraction of A in given mixture = 7/12
Fraction of A in the liquid Added = 0 (since pure liquid B is added)
Fraction of A in the new mixture = 7/16
Ratio of original mixture to B = 7/16 : 7/48 = 3:1
It means for 1 litre of liquid B added, quantity of mixture should be 3 litres.
⇒ For 9 litres of liquid B, original mixture should be = 9 x 3 = 27 litres.
Therefore initial quantity of mixture in can = 27 + 9 = 36 litres.
⇒ A = 7 x 36/12 = 21 litres
⇒ B = 5 x 36/12 = 15 litres
Example 18: A mixture contains wine and water in the ratio 3:2 and another mixture contains them in the ratio 4:5. How many litres of the later must be mixed with 3 litres of the former so that the resulting mixture may contain equal quantities of wine and water?
Example 19: A mixture of 40 litres of milk and water contains 10% water. How much water must be added to make 20% water in the new mixture?
Solution: Method 1: By Alligation: The existing mixture has 10% water. We need to add pure water so water is 100%.
Two mixture should be added in ratio = 80 : 10 = 8:1
It means for every 8 litres of first mixture water to be added = 1 litre
⇒ For every 1 litre of mixture water to be added = 1/8 litre
Hence, for every 40 litres of mixture water to be added = 40/8 = 5 litres
Method 2: Direct formula:
Quantity to be added = Given Solution x (required % value – present % value)/(100 – required % value)
Putting values in above formula: 40 x (20 – 10)/(100 – 20) = 5 litres
Two mixture should be added in ratio = 80 : 10 = 8:1
It means for every 8 litres of first mixture water to be added = 1 litre
⇒ For every 1 litre of mixture water to be added = 1/8 litre
Hence, for every 40 litres of mixture water to be added = 40/8 = 5 litres
Method 2: Direct formula:
Quantity to be added = Given Solution x (required % value – present % value)/(100 – required % value)
Putting values in above formula: 40 x (20 – 10)/(100 – 20) = 5 litres
Example 20: A invested Rs 76000 in a business. After few months, B joined him with Rs 57000. At the end of the year, the total profit was divided between them in the ratio of 2:1. After how many months did B join?
Solution: Let B joined after x months. It means B invested money for (12 - x) years.
⇒ PA : PB = (CA x TA) : (CB x TB)
⇒ 2/1 = [76000 x 12]/[57000 x (12 - x)]
Therefore x = 4 months.
⇒ PA : PB = (CA x TA) : (CB x TB)
⇒ 2/1 = [76000 x 12]/[57000 x (12 - x)]
Therefore x = 4 months.
Example 21: Two partners invested Rs 50,000 and Rs 70,000 respectively in a business and agreed that 70% of the profits should be divided equally between them and the remaining profits in the ratio of investment. If one partner gets Rs 90 more than the other, find the total profit made in the business?
Solution: Method 1: Let total profit is Rs x
70% of the profit divided equally while 30% of the profit divided in the ratio of investment.
⇒ Ratio of investment = 50,000 : 70,000 = 5:7
Share of first partner = 30% of 5x/12 = x/8
Share of second partner = 30% of 7x/12 = 7x/40
Difference in the shares = 7x/40 – x/8 = Rs 90
⇒ x = Rs 1800
Method 2: Direct Formula: Total Profit = Difference in profit x (100/profit % divided in ratio) x (Sum of ratios/Difference of ratios)
⇒ Total Profit = 90 x (100/30) x (5+7)/(7-5) = Rs 1800
70% of the profit divided equally while 30% of the profit divided in the ratio of investment.
⇒ Ratio of investment = 50,000 : 70,000 = 5:7
Share of first partner = 30% of 5x/12 = x/8
Share of second partner = 30% of 7x/12 = 7x/40
Difference in the shares = 7x/40 – x/8 = Rs 90
⇒ x = Rs 1800
Method 2: Direct Formula: Total Profit = Difference in profit x (100/profit % divided in ratio) x (Sum of ratios/Difference of ratios)
⇒ Total Profit = 90 x (100/30) x (5+7)/(7-5) = Rs 1800














No comments:
Post a Comment