Square root - How to find the root of numbers mentally within seconds

SQUARE ROOT

In this post i will explain best square root tricks to solve questions within mind. Square root of any number is a quantity which when multiplied by itself gives the same number. For example: '3' is a square root of '9' which when multiplied by itself produces the number '9'. Every number has two square roots: positive and negative. For example: '9' has two roots +3 and -3. Positive root also known as principal square root. 

Square root of perfect squares are integers while square root of non perfect squares or positive integers are irrational numbers. For example: Square root of '4' is '2' while root of '3' is 1.73205080..... up-to million digits. 

Square Root of Perfect Squares

• Check the unit digit of the given number and write those numbers whose squares give the same unit digit.
• Now neglect last two digits of the given number and find the number whose square is nearest to the given number but not greater.

Example: Find the square root of 324?

Solution:  

Here unit digit is 4, those numbers whose squares give the same unit digit are: 2 & 8.

After omitting last two digits which are “24”, only “3” remains, now write those numbers whose square is nearest to 3, but not greater, and that is “1”.

So answer could be ’12’ or ’18’.


To find the correct one, check the middle term of '12' & '18' containing '5' at units place which is ’15’.
Square of 15 is ‘225’ and number ‘324’ is greater than ‘225’, it means correct answer is 18. Square root of 324 is 18.

Square Root of Non-Perfect Squares

Formula: √x = z + (x - y)/2z
Here x = given number
y = nearest perfect square
z = Square root of nearest (smaller) perfect square

Example: Find the square root of 160?
Solution: x = 160
Nearest perfect square y = 144
Therefore, z = √144 = 12
      ⇒ √160 = 12 + (160 - 144)/(2x12)
                    = 12 + 16/24
                    = 12.66 (approx)

 Method 2 
Nearest perfect squares of 160 are 144 and 169
Difference D1 = 160 - 144 = 16
Difference D2 = 169 - 144 = 25
   ⇒ Ratio D1/D2 = 16/25 = 0.64
   ⇒ √160 = 12 + 0.64 = 12.64 (approx)

 Method 3 
Newton-Raphson Method:  Step 1:  First make a guess 'x' as the Square root of number 'n'. Here number is '6', so i am guessing '2' as a Square root of 6.

 Step 2:  Divide the number by 'x'
   ⇒ 6/2 = 3 

 Step 3:  Take the average of 'x' and this quotient.
   ⇒ (2 + 3)/2 = 2.5 approx.

For better accuracy you can repeat these steps again with 2.5 as new approx value of square root of 'n'.

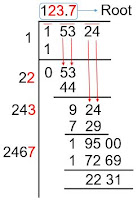
Square Root of any Number (Basic method)

Example: Find the root of 15324?
Solution:  Step 1:  Divide the number into pair of two digits starting from right.
                ⇒ 1, 53, 24 
 Step 2:  Now multiply a number by itself such that product always less than or equal to the given pair. Here 1x1 =1 which is equal to 1.

Here remainder is 0 and quotient is 1. 
 Step 3:  Now multiply quotient with 2 and bring down the next pair which is '53'.

 Step 4:  We need to use same number at the place of ? so that the product must be less than or equal to 53.

 Step 5:  Replace '?' with 2 and we get 44 which is less than 53. Now bring down 24.

 Step 6:  Multiply the quotient with 2.

 Step 7:  Repeat the above steps.

Square Root of 15324 = 123.7

First method always give fast answer but without decimal, it may give right or wrong which depends on options. If all the options of multiple choice question are integers then this method is best to find the square root withing seconds. In case options of multiple choice questions contains decimal numbers, it will be better to use second or third method. These methods will shorten your calculation and you will find square root fast and easily.