Decimal System - How to solve decimal numbers (recurring) within seconds - Math Tricks

DECIMAL NUMBERS

Decimal Numbers are those numbers which contain decimal separator like 10.56, 0.3458 etc. We read it as ten point five, six (=10.56) or zero point three, four, five, eight (=0.3458) etc.

In this post i will explain mathematical operations of decimal numbers like how to add or subtract Recurring decimals quickly, multiplication and division tricks of decimal fractions and methods to convert decimal fractions into vulgar fractions within seconds to shorten the calculation.

Fractions in which the denominators are powers of 10 are known as Decimal Fractions.
For example: 3/10 ; 11/100 etc. We can represent these fractions as 0.3, 0.11 etc.
Fractions in which the denominators are not in powers of 10 can also be converted into decimal numbers.

Types of Decimal Fractions

There are two types of decimal fractions:
 1.  Terminating or Non-repeating: Decimal numbers in which digits don't repeat after decimal are known as terminating or non-repeating decimals. For example 1.023, 0.5648 etc.

 2.  Recurring or Non-terminating: Decimal numbers in which digits or a set of digits repeats continuously are known as recurring or non-terminating decimals. These are also known as periodic or circulating decimal numbers. The repeated digits or set of the digits is known as period of decimal. These are further divided into two types:

• Pure Recurring Decimal: Fractions in which all figures after decimal point are repeated.
  For example: 0.235, 0.3 etc. It has 3 period and 1 period respectively. 

• Mixed Recurring Decimal: Fractions in which some figures recur and some don't. For example: 0.0235, 0.3532 etc.

Rules To Identify Fractions

 1.  If the denominator of any fraction is made up of powers of 2 & 5, that fraction will give terminating decimal.
 2.  If the denominator of any fraction does not contain 2 & 5 as a factor or if the denominator is neither divisible by 2 nor 5, then that fraction will give pure recurring decimal.
 3.  If the denominator of any fraction contains powers of 2 & 5 in addition to other divisors or factors, that fraction will give mixed recurring decimal.

Example: Identify the fractions as terminating, Pure recurring or Mixed recurring decimal fractions:
a.) 29/50 ;     b.) 3/37 ;     c.) 7/12
Solution: In the first fraction 50 =  52 x 2
⇒ It is made up of powers of 2 & 5 only, so fraction is terminating.

In the second fraction 37 does not contains any power of 2 & 5, so fraction will be pure recurring.
       ⇒ 3/37 = 0.081

In the third fraction 12 = 22 x 3
It contains powers of 2, so it will give mixed recurring decimal.
       ⇒ 7/12 = 0.583

Conversion of Recurring Decimal To Vulgar Fraction

 Rule 1:  In case of Pure Recurring decimals, remove the Bar or Vinculum and count the number of digits in the period of decimal. Divide the numerator by the same number of 9's as there are digits in period of decimal.
Example: 0.081
Solution: 0.081 = 081/999 = 3/37

 Rule 2:  In case of Mixed Recurring decimals, remove the Bar or Vinculum and subtract the non recurring digits from the whole number. For denominator write as many 9's as there are digits in recurring period of decimal followed by as many 0's as there are digits in non recurring period of decimal.
Example: 0.328
Solution: Non recurring digits are two, so number of 0's in the denominator will be 2.
Recurring digit is 1, so number of 9's in the denominator will be 1.
          ⇒ Denominator = 900
          ⇒ 0.328 = (328 - 32)/900 = 74/225

Basic: 0.328 = 0.328888...
100 x 0.328 = 32.8888...     (eq.1)
1000 x 0.328 = 328.8888... (eq.2)

Subtracting (eq.1) from (eq.2) we get:
          ⇒ 900 x 0.328 = 296
          ⇒ 0.328 = 296/900 = 74/225

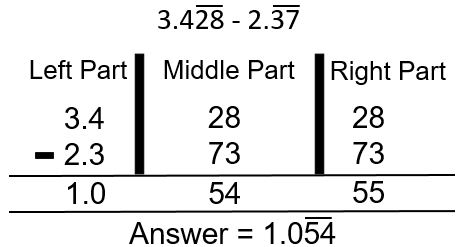
Addition & Subtraction of Recurring Decimal

 Step 1:  Separate the given Recurring decimal into three parts - left, Right and middle part.

 Step 2:  In the left part,  write the integral value with non recurring decimal digits. If first recurring decimal has more non-recurring digits, then write the same number of digits of second number in the left part.

 Step 3:  In the middle part, write the number of digits equal to the LCM of the number of recurring digits in the given recurring decimals.

 Step 4:  In the right part, write the two digits only of the recurring decimals.

 Step 5:  Perform addition or subtraction and put a Bar or Vinculum above the resultant of middle part.

Example: 3.428 + 2.37
Solution: We can write 2.37 as 2.373737...  and 3.428 as 3.42828...

Total number of non recurring digits in the first number are 2 (3.4 rest 28 repeats) and in the second number non recurring digit is 1 (only 2, rest 37 repeats) . So in the left part we have to write '2' digits. So we wrote 3.4 from first number and 2.3 from second number on left side.

Now LCM of recurring digits is 2 because total number of recurring digits in both the numbers are same which are 2 (= 28 & 37)

In the right part we need to write only two digits followed by middle part digits, so we wrote 28 & 73 respectively.

Now perform addition and put Bar or Vinculum above the middle part result.

Second Method:  3.428 = 3 + (428 - 4)/990
                                       2.37 = 2 + 37/99
 ⇒ 3.428 + 2.37 = 5 + 37/99 + 424/990
                             = 5 + 794/990 = 5.802

This method will be very calculative in case of large recurring digits, so first method should be used.

Now Perform subtraction using same method:-

Multiplication & Division of Recurring Decimals

 Rule 1:  If any Recurring decimal is multiplied by a multiple of 10, period of the decimal is not altered.
For example: 3.28 x 10 = 32.828
Explanation: (3 + 28/99) x 10 = 30 + 280/99
                    = 32.828

 Rule 2:  During multiplication with any number which is not a multiple of 10, we need to convert Recurring Decimal into vulgar fraction and then the calculation will be done.
For example: 8.63 x 11 = (8 + 63/99) x 11
                   ⇒ 95/11 x 11 = 95

 Rule 3:  If any Recurring decimal is divided by a multiple of 10, period of decimal remains unaltered, only decimal shift towards left..
For example: 28.65828/100 = 0.2865828

 Rule 4:  When divisor is not a multiple of 10, we can either convert Recurring decimal to vulgar fraction or directly divide them.
For example: 15.231 /7 = 15.2313131.../7
                   =  2.1759018

That's all about decimal numbers or decimal fractions. These are best tricks to add, subtract, divide or multiply Recurring decimals or to convert decimal into vulgar fractions. These methods will be useful during simplification questions ask in various examinations. Try to use basics as well as these new tricks with stop watch to feel the difference of these time saving techniques. Good Luck 👍